 GLAST detector module
GLAST detector module
To:
The Gamma-ray Large Area Space Telescope (GLAST) is a proposed next-generation high-energy gamma-ray telescope for studying emission from astrophysical sources in the ˜ 10 MeV to 300 GeV energy range. The primary scientific targets include active galactic nuclei, gamma-ray bursts, neutron stars, and diffuse galactic and extragalactic high-energy radiation. Like previous high-energy telescopes, GLAST relies on the unambiguous identification of incident gamma-rays by detection of the electron and positron that result from pair creation in a thin converter material. Measurement of the energy and direction of the e+-e- shower provides information about the energy and direction of the incident gamma-ray. In contrast to earlier orbiting telescopes, the GLAST design utilizes modern solid-state particle detector technology and recently developed advanced space-qualified computers. In particular, GLAST uses position-sensitive silicon strip detectors, interleaved between thin converters, to track particles rather than using a gaseous particle tracker. Because of this technical approach, the telescope design can be easily optimized to a range of sizes. For example, accommodation of GLAST within a Delta II size launch system results in an instrument with capabilities well beyond those of EGRET currently operating on the Compton Observatory; namely, a broader energy range, larger effective area, wider field of view, and single-photon angular resolution 2 to 5 times more precise than EGRET's resolution. GLAST will have a maximum effective area of ˜ 8000 cm2 above 300 MeV, a field of view of 2.6 sr, and a single photon angular resolution (rms projected) of 0.3o at 1 GeV, approaching 0.03o above 20 GeV.
In this paper, the GLAST instrument design is described and its observational capabilities are discussed. The current state of instrument development is presented including the results of detailed Monte Carlo simulations of detector interactions with gamma-rays and with various charged and neutral particle backgrounds, and the design and prototyping of silicon strip detectors and low-power VLSI readout electronics.
The Compton Observatory, launched by NASA in 1991, has demonstrated the richness of astrophysical phenomena in the gamma-ray regime (see, e.g., Gehrels, Fichtel & Norris 1994). At the highest energies the Energetic Gamma-Ray Experiment Telescope (EGRET) has moved gamma-ray astronomy from an exploration phase with SAS-2 and COS-B to an established observational field of astrophysics. EGRET has increased the number of identified sources by more than an order of magnitude (Fichtel, et al. 1994). Among these sources are pulsars, supernovae remnants, molecular clouds, and active galaxies. EGRET has provided broadband spectra of these sources, light curves of the pulsars, and has observed dramatic flaring episodes on timescales of a few days in some of the extragalactic sources. There are also many EGRET sources which have not yet been identified at other wavelengths including high latitude sources, most of which are presumably extragalactic, and many sources along the galactic plane. Multi-GeV emission has also been detected from several gamma-ray bursts. This unanticipated discovery has led to new models of the sources of these mysterious cosmic explosions.
The advances in observational capability provided by EGRET are due to the roughly factor of ten increase in sensitive area, improved angular resolution, and broader energy range of EGRET compared to the SAS-2 and COS-B instruments. To continue to advance, high-energy gamma ray astronomy and the scientific understanding derived from it requires a next-generation orbiting gamma-ray telescope with a large field of view and with sensitivity increased and angular resolution improved by factors at least comparable to the enhancements made with EGRET compared to SAS-2 and COS-B.
EGRET was first proposed in the early '70s. The instrument was designed around particle detectors developed during the late '50s and '60s. More than 20 years have elapsed and particle detector technology has continued to advance. In particular, the high-energy physics requirements for 4p sr coverage of collision regions at accelerators, with ever increasing tracking precision in a hostile radiation environment, has led to the development of new, non-gas based technologies. It is not surprising to find that the application of these technologies to the problem of gamma-ray detection in space can lead to large advances. In particular the solid state detector technology known as silicon strip detectors is well suited to an EGRET like application. The results are an instrument which has a large field of view (nearly 2p sr) while at the same time has angular resolution 2 to 5 times more precise than EGRET's. We call this next generation high-energy gamma-ray telescope the "Gamma-ray Large Area Space Telescope" (GLAST).
The technologies of choice allow the telescope to be designed to a range of sizes; accommodation of GLAST within a Delta II size launch system gives an instrument with an effective area - solid angle product more than 40 times that of EGRET. The energy coverage of GLAST pushes below EGRET's cutoff, down to the critical energy of the pair converter material (~10 MeV), and extends upward to ~300 GeV, above which the rate of detected gamma rays becomes very small for any practical realization of an orbiting telescope.
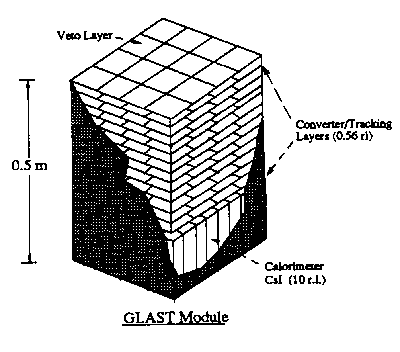
Figure 1 is a schematic diagram of GLAST. Like previous orbiting high-energy gamma-ray telescopes, GLAST relies on the unambiguous identification of incident gamma-rays by recording the characteristic track signature of the e+-e- pair that result from pair creation in layers of thin converter material. Measurement of the energy and direction of the gamma-ray induced shower provides information about the energy and direction of the incident photon. The telescope design consists of three elements: a segmented charged particle anticoincidence shield; a gamma-ray converter/tracker, consisting of thin sheets of high-Z converter material interspersed with silicon strip detectors for particle tracking; and a segmented CsI calorimeter to provide good energy resolution at high energies. The GLAST detector is modular, the baseline design described in this paper consisting of a 7 x 7 array of towers, with each tower containing elements of the anticoincidence shield, the tracker/converter stack, and the calorimeter.
Each plane in the tracker has two sets of strip detectors that can accurately measure the charged particle tracks in two orthogonal dimensions. These tracks can be used to identify gamma-ray interactions, as the showers resulting from gamma-ray conversions have different properties than those caused by high energy hadrons (protons, neutrons, etc.). By observing the pattern of charged particle "hits" in the silicon strip tracker and the energy deposition pattern in the calorimeter, events caused by gamma-rays that enter through the front of the instrument can be distinguished from the much higher fluxes of cosmic-rays and trapped radiation incident on the instrument in orbit. Also, earth-albedo gamma rays are easily identified and eliminated by their directional signature. The combination of larger effective area, wider field of view, broader energy range, and much improved single photon angular resolution, extends the discovery reach of GLAST well beyond that of EGRET. Table 1 lists some of the parameters of GLAST and corresponding parameters for EGRET.
Table 1: Comparison of GLAST and EGRET g-Ray Telescope Parameters
EGRET (1) GLAST Conceptual
Design
Energy range 35 MeV - 30 GeV(2) ˜ 10 MeV - 300 GeV
Energy resolution(3)
10 MeV ... 24%
50 MeV 14% 12%
100 MeV 12% 8%
1 GeV 9% 4.4%
10 GeV 12% 6%
100 GeV ... 18%
Effective Area(4)
10 MeV ... 300 cm2
50 MeV 250 cm2 4000 cm2
1 GeV 1200 cm2 8000 cm2
10 GeV 700 cm2 8000 cm2
100 GeV ... 8000 cm2
Solid Angle 0.15 x p sr 0.82 x p sr
Acceptance(5)
Full Field of View 0.2 x p sr 1.8 x p sr
Point Source
Sensitivity(6)
E>100 MeV 5.4 x 10-8 ph cm-2 1.5 x 10-9 ph cm-2 s-1
s-1
E>1 GeV 1.2 x 10-8 ph cm-2 1.5 x 10-10 ph cm-2
s-1 s-1
E>10 GeV 2.1 x 10-8 ph cm-2 9.5 x 10-11 ph cm-2
s-1 s-1
Single photon position
error(7)
10 MeV - 12.7o
50 MeV 8.4o 5.2o
100 MeV 5.6o 2.5o
1 GeV 1.5o 0.42o
10 GeV 0.5o 0.10o
Point Source Location 5-10 arcmin 0.1-1 arcmin
Volume 4.8 m3 ˜ 2 m3
Mass 1830 kg ˜ 2700 kg
Power 190 W ˜ 1 kW
Lifetime ˜ 4 yr >4 yr
Parameters for the EGRET instrument are from Thompson, et al. (1993) and Walker (1990).
Research to date has shown that a practical instrument of the GLAST scale can be built. The cost of silicon strip detectors has now decreased to the point where large arrays are feasible. Furthermore, developments originally aimed at the use of these devices in multi-TeV colliders have led to the design of electronic readout devices that have low power consumption, so that it is feasible to operate arrays of these detectors on a satellite. In section 2 of this paper, a more detailed description of the GLAST instrument and its expected performance as an astronomical instrument is given along with discussion of some general pair-conversion telescope design considerations. Spacecraft and launch requirements are also discussed.
Any high-energy gamma-ray telescope must achieve sufficient background rejection to distinguish the weakest detectable cosmic gamma-ray flux (i.e., the diffuse high latitude gamma-ray background) from the much larger particle background rates. Extensive Monte Carlo simulations, described in section 3, of the interactions of gamma-rays and various other background particle fluxes with GLAST have been used to evaluate the instrument's performance and background rejection capabilities. The simulations have verified the validity of the pattern recognition method for background discrimination, also described in section 3.
A basic difference between the GLAST concept and previous spark-chamber telescopes is that no hard-wired 'trigger' is required and essentially the signals from all interactions in the instrument are initially accepted. Gamma-ray event selection and processing is done on these signals in several steps, the first set of which are implemented with onboard programmable hardware logic and an onboard instrument computer. Subsequent analysis of telemetered data to extract true celestial gamma-ray events is done on the ground. The GLAST onboard multilevel trigger architecture is described in section 4.
The rich variety of astronomical phenomena in the high-energy gamma-ray sky place strong demands on the performance of the next-generation high-energy gamma-ray telescope. This telescope must have angular resolution that will meet the requirement to identify point sources with objects at other wavelengths, yet have a wide field of view that will permit the study of sources that exhibit extreme intensity variations on timescales from seconds to months or longer. The GLAST design meets both requirements; it achieves half-sky coverage (and nearly daily full-sky coverage in a scanning mode) with more than 106 pixels covering the sky. In section 5, the scientific motivation for and observational breakthroughs likely to be obtained with GLAST are discussed.
In common with EGRET, the GLAST design relies on the unambigious identification of incident gamma rays by recording the characteristic e+-e- pair track signatures that result from pair creation in a thin layer of converter material. Measurement of the energy and direction of the electron and positron provides information about the energy and direction of the incident gamma ray. In contrast to EGRET which uses spark chambers to image the pair tracks, the GLAST telescope design uses position-sensitive silicon strip detectors (nominal resolution of 69 µm) interleaved between the converter layers.
Developments in using semiconductors for particle detection over the past decade are the main technical stimulus for GLAST. In particular, the development of large area silicon strip detectors for use in particle tracking and calorimetry has resulted in working devices now in wide-spread use in major high-energy particle detectors both in the USA and in Europe (Almehed et al. 1991; Berridge et al. 1988, 1990). Much recent innovation was brought about because of the detector challenges that were presented by the Superconducting Super Collider (SSC). Significant among the advances in silicon detector technology is the cost, now < $20/cm2 versus almost $200/cm2 a decade ago (Hylen et al. 1990).
The use of solid-state silicon strip detector (SSD) technology in a pair-conversion gamma-ray telescope offers a number of advantages that include long lifetime, high efficiency, stability, fail-safe operation to many common mode failures, no consumables, operation at relatively low voltages (˜100 volts), simple readout, and a live detector with essentially no dead time that does not require an external trigger. SSDs also have an intrinsically fast time response and are relatively radiation hard. Most important, the fine segmentation possible with this technology allows precision coordinate measurements as well as the ability to distinguish closely spaced tracks. In operation, these detectors have excellent signal-to-noise (typically 20:1) and they provide a digital data stream that allows for simple and flexible high-level software triggers. Monitoring and calibration of detector performance is also relatively straightforward, especially when compared to gaseous tracking devices.
The GLAST design is based on industry standard silicon. This means 6 cm x 6 cm tiles with a thickness of 300 to 500 µm. The tiles have diode strips implanted on them to establish the readout pattern. Tiles may be "ganged' together to reduce the overall channel count. The strip separation (or pitch) commonly in use in high energy physics is ~50 µm but for the tracking portion of GLAST, 240 µm strips will suffice. GLAST will require approximately 75 m2 of silicon strip detectors in the converter/tracker, with a total of 1.3 x 106 readout channels.
The GLAST detector is modular, consisting of an assembly of 24 cm x 24 cm towers. A 7 x 7 array of these towers is envisioned, resulting in a large area detector with mass, volume, and power requirements permitting launch on a Delta II. Figure 1 shows the design of a GLAST detector module and Figure 2 is a comparison of GLAST with EGRET. The modular design of GLAST has the advantages associated with a large degree of redundancy.
There are several aspects of the GLAST design that are significant departures from previous orbiting high-energy gamma-ray telescopes operating in the pair conversion regime. These include
The various parts of GLAST are discussed in more detail in the following paragraphs.
While the GLAST design uses discrete radiators, telescopes have been proposed that use a distributed active radiator for the converter; for example, a drift chamber using high Z gas (Xenon) as the converter. As discussed in Appendix A, the angular resolution achievable with discrete radiators is superior to that obtainable with a continuous converter. In the limit that small-angle multiple scattering dominates over measurement errors, the ratio of the area of the error ellipse for the continuous case to that for the discrete case is ˜ 4.2(xc/xd), where xc and xd are the thicknesses, in radiation lengths, of a single detector measurement layer for the two cases. Stated another way, for such detectors with radiator thicknesses adjusted to give equal angular resolutions the discrete case will have an event rate approximately 4.2 times larger.
Figure 1. Conceptual design of a GLAST detector module.
Figure 2. Comparison of GLAST and EGRET.
Behind each radiator in the GLAST tracker is a tracking layer consisting of a pair of single-sided silicon strip detectors that provide (x,y) position determination. The radiator layers are then followed by two planes of (x,y) silicon strip detectors. Double-sided (x,y) strip detectors could be used but the use of single-sided detectors saves on cost. The 240 µm strip pitch will result in an rms position resolution of sp~69 µm in x and y. The electron and positron from a just converted photon will make one hit in the silicon immediately following the radiator thus precisely locating the conversion point. The multiple scattering occurring in the radiator and the intrinsic opening angle of the pair will typically cause two hits in the next layer of silicon (which is after the next radiator). Multiple scattering in the second radiator is of little concern because it is located directly on top of the second layer of silicon. The intrinsic two hit resolution of 480 µm allows for more accurate tracking of the initial pair. This is to be compared with the relatively poorer multi-track resolution of a gaseous tracking device, such as the EGRET spark chamber, in which the two hit resolution is typically about 3 mm. The best two-track resolution reported (Bettoni et al. 1983) in a high pressure drift chamber approaches 700 µm, but only for the particularly favorable case of tracks that are perpendicular to the drift direction. Typically > 2mm two-track resolution has been achieved in full scale experiments.
For very high photon energies the rms projected angular resolution of the baseline telescope configuration is limited to ~0.03o by the strip pitch and spacing between planes. For the total 0.56 radiation length thickness of the tracker/converter, the probability of a photon converting is 0.35 (above 1 GeV). The final design of the tracker/converter will clearly be a tradeoff between having more layers (greater conversion probability), thinner layers (less multiple scattering), smaller strip pitch (more electronics and power), and greater spacing between the layers (better angular resolution but a worse aspect ratio/solid angle for the whole detector).
The precise determination of the relative alignment of detector planes can be established in-flight using high-energy cosmic rays because they have straight-line trajectories. Absolute determination of the instrument reference axis direction relative to the satellite attitude reference system can be accomplished in-flight by observation of known strong gamma-ray sources (e.g., Vela, Crab, Geminga, etc.).
For a typical source, the GLAST sensitivity will permit measurement of spectra to an energy approximately 6 times higher than the maximum energy detectable with EGRET (for a given confidence level). Thus GLAST should be designed to have a better resolution at high energies than EGRET. There is clearly an optimization between weight constraints and the desire for a thicker calorimeter. In the baseline design, the calorimeter for each module consists of an array of 64 crystals, each 3 cm x 3 cm x 10 radiation lengths, to improve the high-energy resolution.
The GLAST instrument design presents minimal technological challenges. Among these, the most difficult are:
Low power, low-noise front-end electronics are important for GLAST because of the large number of electronic channels. Custom VLSI chips have been developed for the readout of silicon strip detectors in high energy physics applications. These systems usually achieve at least a 15:1 signal to noise for a minimum ionizing track passing through the 300 µm thick totally depleted p-i-n silicon strip detector. Detectors have been daisy-chained together to achieve lengths typically 18 to 24 cm, similar to that used in the GLAST design. Varieties of readout chips include both the preamplifiers, discrimination, data storage, and sparse readout capability necessary for the enormous number of channels. The chip dice are mounted on or adjacent to the silicon strip detector and individual channels (typically 64 or 128 channels/chip) are bonded to the silicon strips.
A substantial amount of design work toward large silicon-strip tracking systems was undertaken for the SSC. The SSC designs yielded power levels of ~1 mW/channel with ~10 nsec risetimes. It is clearly desirable to reduce this power. With long shaping times (˜1 µs) being sufficient for GLAST, it is advantageous to use FET amplifiers (rather than bipolar amplifiers) that can be operated with relatively low bias currents. Lowering the FET bias current can introduce increased FET voltage noise but this can be offset by reducing the Si strip capacitance. The capacitance can be reduced by minimizing the interstrip capacitance with narrow strip implants (Barberis et al. 1992) and using 500 µm thick wafers. Thicker wafers would also give a larger signal, which would allow the use of longer strips and would reduce the channel count but would increase the full depletion voltage unless the detectors are fabricated from higher resistivity silicon.
Over the past year, we have been developing and evaluating prototype designs of the GLAST front-end electronics. One of these designs, developed by collaborators at Los Alamos, starts with the SSC front-end architecture that consists of five stages: a low-noise preamplifier stage; a shaper stage to limit the bandwidth; a comparator stage to discriminate the signal; a digital buffer to store the time stamp of the discriminated signal; and a data compression and transmission stage. This design, optimized for the speed and noise performance needed for GLAST using 500 µm thick silicon wafers, achieves a power per channel of 150 µW. Prototypes of this design have been fabricated and are being evaluated. Another chip, based on the SVX II design from LBL, has been evaluated by the group at U.C. Santa Cruz. It meets the GLAST noise requirements with power dissipation of less than 500 µW per channel. A third design, developed by the INFN Trieste group, also achieves about 500 µW/channel.
Table 2 lists the channel counts and estimated power usage for the tracker/converter, calorimeter, and on-board computers, assuming a conservative 300 µW/channel and 24 cm effective strip length. These numbers are our present estimates and will likely be reduced with an optimized readout electronics design.
Table 2: Power estimates for the GLAST instrument.
Layer type Channels per layer # of Power
layers (W)
g-ray converter: 2 single-sided 2 x 49 x 13 390
Si layers, per converter layer, with 300 (24cm/0.24mm)=98,000
µm pitch
On-board computers: RH-32 or RH6000 30
CsI Calorimeter: photodiode readout 49 x 2 ph x 8 xtls x 1 250
8 xtls = 6272
TOTAL 670
The parameters of the GLAST instrument are preliminary and will continue to be refined in the course of subsequent R&D. The lower end of the GLAST gamma-ray energy range (˜ 10 MeV) will be determined primarily by the properties of the tracking/converter stack and the calorimeter. The upper end is determined by the energy at which the number of gamma-rays expected to be detected in a reasonable exposure time is small. For bright sources this energy overlaps the lower end of what is observable with ground-based atmospheric detectors.
Figure 3 summarizes the instrument's effective area versus energy, the angular resolution (space angle for 68% containment) versus energy, and the energy resolution versus energy for an on-axis source. These instrument parameters were determined with the Monte Carlo simulation described in section 3. Inefficiences due to background rejection analysis cuts have been included. The angular resolution was computed from the on-axis point-spread function determined by the Monte Carlo simulations. The off-axis effective area of GLAST is essentially given by the geometric projection of the effective area at normal incidence. The energy resolution shown is the equivalent Gaussian s determined from Monte Carlo distributions of the energy deposited in the calorimeter, corrected for energy loss in the tracker. Tracker corrections become increasingly important below 100 MeV. Fluctuations of the shower leakage out the back of the calorimeter begin to become important above 10 GeV. The energy measurement reach of GLAST would extend into the multi-TeV range with a thicker calorimeter, but the number of photons expected does not justify the extra weight. With a 10 r.l. thick calorimeter, simulations show that an energy measurement is still possible (s ˜33%) at 800 GeV.
Figure 3. GLAST and EGRET effective area, angular resolution, and energy resolution versus energy for photons incident normal to the detectors. Also shown are the relative effective areas (@ 1 GeV) versus the angle of incidence. Inefficiencies due to analysis cuts for background rejection have been included.
At low energy, the response of a gamma-ray pair conversion telescope is bounded from below by energy conservation. The pair production cross section is essentially zero for gamma-rays below 2 MeV. Pair production, however, does not dominate the total photon interaction cross section until the gamma-ray has an energy greater than the critical energy of the material through which it is passing. The critical energy, approximated by
Ecrit = 800 MeV/{Z + 1.2}},
is 9.6 MeV for Pb, 10.8 MeV for Ta, 14.5 MeV for Xe, and 26.5 MeV for Cu. We have choosen Pb for the baseline GLAST design as it has the lowest critical energy of any practical radiator material.
While the above limit sets a lower bound on the gamma-ray energy that can be detected which depends on the physics of the pair conversion process in a given material, the layout of the pair telescope has the dominant effect. All pair-conversion telescopes have lower efficiency for the detection of lower energy gamma rays. This is because the products from the initial conversion become too soft to allow reliable track reconstruction and often either multiple scatter out of the tracker or range out before striking the calorimeter.
Placing material and distance between the tracker and the calorimeter makes these effects worse. In particular, this space is the location of the TOF system in in instruments such as EGRET. A separation of ³ 50 cm is required for the TOF to effectively establish forward-backward directionality with ˜nanosecond time resolution. If this space is filled with vacuum the losses can be minimized. However, this is not the case for both spark chamber and drift chamber designs. For example, in spark chamber systems, a minimum of two layers of TOF scintillators are required ( ³ 1 cm plastic per layer), while for drift chamber detectors the TOF system typically resides in the gas volume along with the calorimeter to avoid the gas vessel walls.
One can crudely estimate the lower energy cutoff of gamma-ray conversion telescopes as follows. The amount of material which must be penetrated is estimated by taking ½ the total thickness of the radiator stack plus the material between the tracker and the calorimeter. The latter includes material in the TOF (and to a lesser extent the gas and additional tracking planes) in the case of EGRET. The mean energy of the higher energy particle in a gamma-ray conversion pair is 75% of the energy of the gamma-ray, Eg. This particle must penetrate through to the calorimeter. In Figure 4 the corresponding minimum gamma-ray energy as a function of the amount of material to be penetrated, expressed in radiation lengths, is plotted. The points on this curve corresponding to EGRET and GLAST are also indicated. Again we see that telescopes requiring a TOF significantly increase this lower bound, while the GLAST design minimizes the amount of material, providing the lowest achievable low-energy cutoff for a pair conversion telescope. While the effective area of GLAST (see Fig. 3) falls rapidly below this energy, it none the less has significant response down to the critical energy (300 cm2 at 10 MeV).
Figure 4. Comparison of the low-energy cutoffs for GLAST and EGRET.
Perhaps the most dramatic departure of the GLAST design from previous ones is the large field of view afforded by the elimination of the TOF system. This has important implications for the way the science from the mission can be optimized. For example, instead of pointing at specific sources, the observing live time can be maximized by scanning with the instrument always pointed away from the earth (zenith pointing). In each orbit most of the sky will be scanned, and transient phenomena are more likely to be detected. An initial one year all-sky survey may best be carried out in this mode. For other objectives, such as mapping of a particular region of the sky or studies of particular objects, a pointed mode is optimum because the on-axis effective area is maximum and the best angular resolution is obtained on-axis. For energies below about 1 GeV, where multiple scattering is most important, the rms projected angular errors for photons incident at an angle q from the normal are given approximately by qrms(q) = qrms(0)/÷cosq. This scaling is verified by the Monte Carlo simulations.
Restricting the discussion to detectors with planar geometries, the ideal detector would be one with essentially no thickness. This ideal device would be sensitive over 2p sr with an effective area decreasing as the cosine of the angle away from the normal to the detector plane cosqn. However, real instruments have a finite thickness. The approach to the ideal case occurs as the the ratio of the minimum tracker thickness (D) to its width (W) is maximized. The fraction of sky coverage of the real detector compared to the ideal case is approximately given by
F = 1 - cos(p/2 - tan-1(D/W)).
The angular acceptances determined from a Monte Carlo study of detector designs of varying W/D ratios are shown in Figure 5, with the values for EGRET and GLAST indicated.
Figure 5. Angular acceptance as a function of geometric aspect ratio.
The EGRET aspect ratio is approximately unity because of the time-of-flight system (TOF). Primarily because it does not require a TOF, GLAST has a much more favorable aspect ratio that results in an acceptance approaching that of an ideal detector. The predicted acceptance (see Table 1) of GLAST, based on Monte Carlo simulations that include analysis cuts for background rejection, is somewhat less than the ideal case.
The estimated mass of the 2.8 m2 GLAST is ~2700 kg. This consists of about 2400 kg in the calorimeter and 300 kg in the converter/tracker. EGRET's mass is 1830 kg. The volume of GLAST is easily compatible with a Delta II launch. With respect to mass, a Delta II (7920/25) can deliver a total mass of about 4700 kg to a 28.5o inclination, 500 km orbit (Loftus & Teixeira 1992). Without a more detailed system study including a preliminary spacecraft design, it is difficult to accurately assess the launch requirements of GLAST. Based on the type of payload, the present best estimate is that the mass of GLAST is compatible with a Delta II launch.
Because of the very large field of view of GLAST, the spacecraft pointing requirements are very relaxed; pointing accuracy and stability of a few degrees is easily sufficient. For a wide field of view instrument a zenith pointing mode is desirable as well so that the instrument always points away from the earth. In this mode the GLAST instrument would scan nearly the entire sky during each orbit. This would maximize its sensitivity to transient phenomena. A pointed mode is also desirable for obtaining optimal sensitivity to selected sources.
Given the GLAST point spread function, simulations indicate (see section 5) that in a one-year all-sky survey, the typical error box radius of an isolated high galactic latitude source detected at 5s or greater will approach 10 arcsec. Therefore, it is desirable to have knowledge of the spacecraft pointing direction to better than this accuracy. It is not necessary to construct the GLAST tracker with the internal alignments of the planes, etc., maintained to a comparable accuracy. As mentioned earlier, high-energy cosmic ray trajectories can be used to accurately establish the internal alignment of the detector planes.
GLAST will have about 100 times the gamma-ray data rate of EGRET. Simulations and use of a simple on-board triggering scheme such as the one discussed in section 4 suggest that the maximum downlink data rate needed will be less than 100 kbps. Development of efficient on-board processing will likely reduce this rate by a factor of 4. The actual rate will depend on several considerations such as how much back-ground rejection is done with on-board event analysis versus analysis on the ground. As a more detailed event-processing architecture for GLAST is developed, the estimates of the telemetry rate needed will be refined.
AND BACKGROUND REJECTION
Extensive Monte Carlo simulations to evaluate the instrument performance including its effective area, angular resolution, and energy resolution have been done. Most important, these simulations have verified the background rejection capabilities of the instrument and have resulted in development of relatively simple and effective pattern recognition algorithms to distinguish valid gamma-ray events from the much larger particle background rates.
The Monte Carlo simulations have been done using a state of the art package known as Gismo (Atwood et al. 1992). Gismo, written in the object-oriented language C++, includes QED interactions adapted from the EGS4 code (pair production, bremsstrahlung, Compton scattering, Möller scattering, Bhabha scattering, pair annihilation, etc.; Nelson, et al. 1985) and hadronic processes adapted from the Gheisha code (proton-nucleus interactions, p-nucleus interactions, po decay, charged Ks decay, neutral Ks decay, etc.; Fesefeldt). Showers in the GLAST detector simulation were followed down to a 500 keV kinetic energy cutoff. The intrinsic facility built into Gismo to vary detector parameters has been of considerable importance in the Monte Carlo studies. Both the EGS4 and Gheisha codes have been extensively tuned by fits to data from many experiments. More than 106 simulated events (gammas, protons, electrons, neutrons) have been generated to assess the performance of the baseline instrument design.
In the simulations, the full GLAST detector is built up from 49 identical tower modules. Many details of the detector geometry that can affect the instrument performance have been included in the simulation, for example, material representing the readout electronics in each module tracking plane; material representing structural support elements and material necessary for thermal control in each module; finite thickness of the converter planes and the silicon-strip detectors; dead area (˜300 µm) around the edge of each 6 cm x 6 cm Si strip detector wafer and the gaps between modules; segmentation of the CsI calorimeter sub-assembly for each module.
Figure 6(a) shows a simulated 1 GeV gamma-ray event in GLAST. Neutral particles are shown as white lines and charged particles are shown as black lines. In this case the gamma-ray came in the front of GLAST. Figure 6(b) shows the resulting hit pattern and energy deposition in the CsI calorimeter. Each silicon strip detector hit is shown as a horizontal line, the length of which is proportional to the pulse height in the strip. Except for the pulse heights in the silicon strips, this is the event information that is used for subsequent analysis. We have chosen not to use pulse height information from the tracker due to the added complication in the readout. Figures 6© shows an event due to a 15 GeV proton entering the back of GLAST and Figure 6(d) shows the resulting hit pattern and calorimeter energy deposition. The expected cosmic proton flux is expected to peak near 15 GeV for an orbit like that of the Compton Observatory.
The 15 GeV proton generated a very different hit pattern in the detector compared to the gamma-ray event. In particular the proton generated charged particle tracks in the calorimeter and the tracker that left several hits in the front silicon veto layers. There are a number of other quantitative differences between typical valid gamma-ray events and particle background events that can be exploited to achieve adequate background rejection. These are discussed in more detail below.
Fig6 (a) 1 GeV gamma ray event.
Fig 6(b) 1 GeV gamma-ray hit pattern and energy deposition
Fig 6(c)c: 15 GeV proton entering the back of GLAST
Fig6(d)d 15 GeV proton event hit pattern and energy deposition
Figure 6. Monte Carlo simulated events and hit patterns in GLAST tracker and calorimeter.
In low earth orbit many charged and neutral particles will impinge on GLAST. In fact the true extra-solar system gamma-ray signal constitutes a very small portion of the overall rate. When compared to the diffuse extragalactic gamma-ray flux, the cosmic ray background is approximately 104 times larger at the same kinetic energy. While the overall rate of these particles is easily accommodated by modern high-energy physics particle detector data acquisition systems, the data volume produced would be prohibitive to downlink to the ground for analysis. Hence some discrimination is required in orbit. EGRET uses two hardware systems to veto these backgrounds: 1) an anti-coincidence shield, and 2) a time-of-flight (TOF) system. The first of these rejects events caused by charged particles entering through the field-of-view of the detector, while the TOF system establishes the directionality (i.e., that the event was coming from the front). These systems, together with a measurement of energy deposition in the calorimeter, provide a trigger for the spark chamber and subsequent data acquisitions.
Spark chamber-based devices require these triggering systems because each trigger degrades the gas, and the onboard replenishment system contains a limited number of refills. Hence to conserve gas and extend the instrument lifetime, the raw trigger rate must be minimized. Also since spark chambers typically have 100 msec recharging time, the trigger rate must be limited to minimize the dead time.
With GLAST, a hard-wired 'trigger' is not required and essentially the signals from all interactions in the instrument are initially accepted. The GLAST trigger is multilevel with the initial event acceptance criteria implemented with programmable gate arrays while subsequent computer analysis based decisions are done partially inflight and partially on the ground, depending on complexity. The event definition and background rejection is highly flexible and can be tuned even during the mission to cope with unexpected situations or new opportunities. The on-board multilevel trigger architecture is described in more detail in section 4.
An important part of the GLAST instrument concept is that neither a TOF nor a monolithic anti-coincidence shield is used. The reason behind abandoning a monolithic veto counter is to minimize the degradation in the effective area as the energy of the gamma rays increase. As shown in Figure 3, for energies above ˜1 GeV, the GLAST design has a higher efficiency due to the elimination of self vetos arising from shower back-splash from the calorimeter. The solution used in the GLAST design is to have an anticoincidence layer with tracking capability. Instead of demanding a trigger in which nothing appears in the anti-coincidence shield, in GLAST no hits must occur in the veto shield within about 10 cm of the projected track(s). The lack of a monolithic charged particle shield in the GLAST design also removes a large target for soft photons and electrons (positrons) that would otherwise kill a temporally coincident gamma-ray event trigger.
In the following sub-sections we discuss the background rejection capabilities of the GLAST design and show that it provides excellent rejection. The particles encountered in orbit come from five main sources, which may be considered separately: cosmic rays, the Earth's trapped particles, solar flares, albedo gamma-rays and neutrons from the Earth's atmosphere, and interactions in the spacecraft.
Figure 7. The energy spectrum of cosmic-ray protons expected for an orbit with 450 km elevation and 28.5o inclination.
Events are required to pass through at least one live layer and have no hits within 10 cm of the track projection. In this way gamma rays are allowed to enter the sides as well as the front with a subsequent increase in solid angle coverage. This "veto" cut eliminates only a few percent of the gamma-ray events and those are mostly events which convert in the front veto layer or enter the side and convert in the first converter crossed. The efficiency of this cut for rejection of charged particles entering the front of the instrument is greater than 104 to 1 (inefficiencies are caused by multiple scattering for tracks near edges). Monte Carlo generated distributions of the minimum distance of closest approach (DOCA) of veto layer hits to the reconstructed event trajectory for proton events and for gamma rays are shown in Fig. A1. The protons were generated over the full sky using the spectrum in Figure 7, while the gamma rays shown were all generated at 100 MeV (other energies are statistically identical).
From Figure 8 it is seen that a rejection of ˜250:1 is obtained for proton events, while for gamma rays only a few percent are eliminated (after the minimum number of veto layers cut). We estimate the rate for these stiff cosmic ray events on GLAST will be ˜6000 s-1. The reduction by a factor of 250 reduces the event rate to about 30 s-1. This is the "level 2" trigger described in Section 3.2. It can be implemented with onboard processing and requires ˜15 MIPS of processor power. Estimating that each event on average requires 0.4 kbytes, this gives a data rate to the ground of less than 100 kbits/sec.
Figure 8. Comparison of the distribution of the distance of closest approach in veto layers for gamma-ray and hadron events. The accepted events from this analysis cut are those in the shaded region (i.e., no veto layer events within 10 cm of the projected track).
The cosmic rays which remain after this initial processing mainly originate from incoming trajectories that strike the calorimeter directly. The calorimeter presents the largest target on the spacecraft and also has the best solid angle coverage by the tracker. Cosmics can mimic gamma-ray events by interacting in the material of the calorimeter, sending one or more soft secondaries into the tracker.
The following additional analysis cuts can be made in the data analysis on the ground. These cuts could also be implemented in orbit but would require additional onboard processing capability. Events with stiff secondaries penetrating the tracker are mostly killed by the veto cut described above. The soft tracks often range out in the tracker and could easily be eliminated by measuring the energy loss in the silicon strip detectors. We have chosen not to use pulse height information from the tracker due to the added complication in the readout. The soft tracks also repeatedly undergo multiple scatterings, and the next sequence of cuts tends to eliminate them by demanding "good" track quality for the "best" track found in the event. We first eliminate events that have a missing layer in the first planes crossed after conversion or that have more than one missing layer overall. Next we require that the c2 for the best fit track be less than 10 per degree of freedom. Multiple scattering dominates the hit errors in most cases and is estimated from the energy deposited in the calorimeter. The c2 distribution for the remaining proton events and valid gamma rays is shown in Figure 9. At this point 10-3 of the cosmic ray events remain, while ˜95% of converting gamma-ray events are left.
The information in the calorimeter is then used to achieve even greater cosmic-ray rejection. The baseline GLAST calorimeter design is segmented into 3 cm x 3 cm x 18.6 cm crystals with 64 crystals per module (3136 total). Hence each crystal is somewhat larger than one radiation length across and ten radiation lengths long. The main advantage of this segmentation is the increased cosmic-ray rejection it provides based on the pattern of energy deposition. Hadronic interactions tend to be diffuse and spread among many crystals, while electromagnetic showers are compact, typically a Moliere radius wide (˜2 cm in CsI). We analyze the calorimeter energy pattern assuming an elliptical pattern and fitting for the major and minor axis. The energy width is then calculated about the major axis of the fitted ellipse. Cosmic rays tend to have wider deposition patterns than photon-induced showers, and a cut is made based on this distribution. The event rejection factor for cosmic rays after these cuts is 3 x 10-4, and the gamma-ray efficiency is essentially unchanged.
Figure 9. Comparison of the c2 distribution for gamma-ray and hadron events.
The next analysis cut combines the information from the tracker and the calorimeter. The best fit track is projected into the calorimeter to a depth corresponding to shower maximum. The x,y location of this point is compared to the energy centroid in the calorimeter, and the distance between them is corrected by a function of measured energy (to make the resulting quantity approximately independent of energy). The motivation behind this cut is that the tracker and calorimeter will correspond quite well in the case of a photon-induced shower, but this correlation is washed out for a hadronic interaction in the calorimeter. The resulting distributions for cosmic rays and protons are given in Figure 10. With this cut, the cosmic ray background is reduced by another factor of 3 (or 10-4), and the gamma-ray efficiency is reduced to 92%.
Figure 10. Result of matching the calorimeter hit with the tracker pattern for gamma ray and hadron events.
The remaining background events mostly fall into three categories: 1) calorimeter interaction with a soft "stub" which ranges out in the tracker and passes the track cuts (thus stopping the stub); 2) calorimeter interaction with a prong near the edge of the tracker which multiple scatters out the sides and passes the veto cuts; and 3) a calorimeter interaction producing a stub which interacts in the tracker in a manner that leaves no hits to be caught by the veto requirement.
To reject these classes of background events we examine the hit pattern around the best fit track. All of the cases listed above have the common trait of producing an isolated track. On the other hand, gamma-ray events, by the nature of their origin, produce multiple, closely associated tracks. The excellent two track resolution afforded by the silicon strip detectors can pick up the presence of other tracks. Two cuts are designed to capitalize on this feature: 1) gamma-ray events start with a single hit, and 2) around the best fit track in gamma-ray events there should be extra hits. The first cut is effective at eliminating interacting stubs, while the second eliminates stopping stubs and prongs that multiple scatter out the sides of the tracker. These last two cuts improve the rejection to 3 x 10-5 overall, but for events registering ³100 MeV, the rejection rate is 5x10-5. These cuts still leave about 81% of the on-axis gamma rays (62% averaged over the full acceptance).
While the overall initial data rate could easily be accomodated by modern ground-based particle detector data acquisition systems, the data volume would be prohibitive to downlink to the ground from an orbiting experiment. It is essential to provide adequate background discrimination in orbit to lower the data rate. On the other hand a complete on-board analysis of events is inappropriate in view of the on-board computer power necessary and also because it is undesirable to unnecessarily discard information.
Event processing and selection is done in several steps:
Figure 11. GLAST Onboard Event Trigger Architecture
The pattern recognition aspect of the GLAST design is also a significant departure from instruments such as COS-B or EGRET that have a hardware trigger utilizing a time-of-flight system (TOF) to determine the direction of the e+-e- pair. Monte Carlo studies, discussed in detail in Section 4, have resulted in development of relatively simple and effective pattern recognition algorithms to distinguish valid gamma-ray events from the much larger background rates due to cosmic-ray protons, albedo gamma-rays, etc. The most challenging background rejection task is to recognize protons and albedo gamma-rays that enter thru the sides and back of the instrument. With the pattern recognition algorithm developed so far, we are confident of achieving rejection ratios of better than 5x104:1, insuring that such backgrounds are below the isotropic diffuse gamma-ray background. This algorithm accepts valid gamma-ray events with an efficiency approaching 79%, resulting in an on-axis effective area of 5000 cm2 at 50 MeV and 8800 cm2 at 1 GeV.
High-energy gamma rays are excellent probes of the most energetic phenomena in nature, that typically involve dynamical non-thermal processes and include interactions of high energy electrons with matter, photons and magnetic fields; high energy nuclear interactions; matter-antimatter annihilation and possibly other fundamental particle interactions. High-energy gamma rays are emitted over a wide range of angular scales from a diverse population of astrophysical sources - stellar mass objects, in particular compact objects such as neutron stars and black holes; the nuclei of active galaxies that likely contain massive black holes; interstellar gas in the galaxy that interacts with high energy cosmic rays; the diffuse extragalactic background; supernovae that may be sites of cosmic ray acceleration; gamma-ray bursts; and the Sun which during active periods can produce high-energy gamma rays. Many of the sources exhibit transient phenomena, ranging from the few second timescale of gamma-ray bursts to AGN flares lasting days or more and often radiate the bulk of their power at gamma-ray energies.
Observations of high energy gamma rays provide unique astrophysical information. For example:
The high-energy gamma-ray sky presents a diversity of astrophysical phenomena. Because of its larger area, wider field of view, better angular resolution, and broader energy range compared to EGRET, the GLAST instrument is well suited to the study of high-energy astrophysical phenomena that occur over a broad range of angular and temporal scales. In the following subsections, the observational breakthroughs likely to be obtained with GLAST in several of the areas mentioned above are discussed.
With detections (sig. > 5s) of more than 30 active galaxies, EGRET has opened gamma-ray astronomy to the study of extragalactic sources (see von Montigny et al. 1995 for a summary). Most of these sources, distributed over a wide range of redshifts (0.03 to 2.28), have characteristics of the blazar class of AGN (BL Lacs, OVV and HPQ quasars) and many of them are associated with superluminal radio sources. In many of the sources the apparent gamma-ray luminosity is dominant over the flux in lower energy bands and exhibits extreme variations in intensity on timescales from days to months. These time variations imply a source significantly smaller than the smallest resolved radio feature. The photon spectra in the EGRET energy range are generally well-represented by power laws in energy with a wide range of photon spectral indices (a= 1.6 to 2.6, where dN/dE µ E-a) and little or no indication of high energy spectral breaks.
Ground-based TeV observations of several of the EGRET gamma-ray loud AGNs, particularly 3C 279 and Mkn 421, have also been made. A detection of Mkn 421 above 0.5 TeV was reported (Punch et al. 1992). While 3C 279 is a relatively strong EGRET source by comparison, it was not detected in the TeV range, indicating a very strong spectral break above the EGRET energy range. This break has been interpreted as due to attenuation of high energy photons by g-g pair production processes occuring in the intergalactic IR radiation field.
The nuclear activity in AGNs is widely believed to be ultimately powered by accretion onto a massive black hole (for reviews, see Rees 1984; Begelman, Blandford, & Rees 1984). Most of the viable models for gamma-ray emission involve beamed emission from a jet of highly relativistic particles that originate near the black hole central engine. While there appears to be little doubt that relativistic jets are involved, the mechanisms responsible for collimating and accelerating the jets are still speculative. Indeed, there is still major uncertainty about whether the jets are primarily made of an electron-positron plasma or an electron-proton plasma. Most models of the high energy emission involve inverse Compton scattering of low energy photons from a population of relativistic electrons in the jet. Some models involve a cascade that begins with photomeson production by very high energy protons (³ 107 TeV) that are accelerated by diffusive shocks in the jet (see von Montigny et al. 1995 for a recent review of these models).
Despite the importance of the EGRET blazar discoveries, understanding of the gamma-ray emission mechanisms in these sources is limited by current instrumental capabilities. With GLAST:
EGRET has also detected (sig. > 5s) more than a dozen high latitude sources for which no strong candidate identifications have been made. They have spectral and temporal properties similar to the gamma-ray emitting blazars (Hartman et al. 1993). This suggests that either they are also blazars, in which case either radio brightness need not accompany gamma-ray brightness, or the objects brighten in radio by as much as an order of magnitude around the time of a gamma-ray flare, or these sources are members of a different, as yet unidentified, source class.
Even before CGRO it was known that at least the Crab and Vela radio pulsars were emitting pulsed gamma rays above 30 MeV. EGRET observations have so far added PSR 1706-44 (Thompson et al. 1992), Geminga (Bertsch et al. 1992), and PSR 1055-52 (Fierro et al. 1993) to this list. Geminga was known as a strong gamma-ray source from earlier observations but its identification as a pulsed gamma-ray source was not made until the pulse period found for the Einstein source 1E 0630+178 (Halpern & Holt 1992) was also found in EGRET data. Geminga is unusual in that it is not observed as a radio pulsar.
It is well established that radio pulsars are rotating neutron stars with strong magnetic fields. Current models of gamma-ray emission from pulsars fall into two general categories. In the outer gap models (Cheng, Ho & Ruderman 1986), the gamma-ray emission originates in the outer magnetosphere, far from the star's surface. In the polar cap model (Daugherty & Harding 1982), the gamma rays are emitted via curvature and synchrotron radiation in strong magnetic fields just above the polar caps. A pair cascade develops until the radiation can escape. These models were developed primarily to explain gamma-ray emission from the Crab and Vela pulsars which are young pulsars with strong magnetic fields. The detailed information provided by EGRET has significantly promoted theoretical models of pulsars (e.g., Romani & Yardigaroglu 1994, Sturner & Dermer 1994, Daugherty & Harding 1994).
GLAST would detect about 60,000 photons above 20 MeV from the Crab during a 1 month observation. Given the large acceptance of GLAST, many more photons than this would be detected during a typical year long observing program. In the case of the Crab, GLAST could also observe in detail the unpulsed nebular component in the predicted synchrotron-self Compton transition region (DeJager & Harding 1992). EGRET has already detected unpulsed Crab radiation near 1 GeV in which there is a hint of the spectral turnover expected in the transition region (Nolan et al. 1992). The models also suggest the possibility of time variability of the unpulsed emission. Again, the large acceptance of GLAST affords the opportunity to address this question.
Any prediction of the number of rotation-powered pulsars GLAST would detect is obviously model-dependent. In the case of relatively young pulsars with strong surface magnetic fields, the EGRET detections indicate that the magnetospheric efficiency h for conversion of spin-down power into high-energy gamma rays increases with the pulsar's characteristic age t, ranging from 10-4 for the Crab to near unity for Geminga and PSR 1055-52 (Fierro et al. 1993). Based on EGRET upper limits, there is also some indication that gamma-ray emission turns off in high-field pulsars older than about 106 years. This behavior is expected in some versions of the outer gap and polar cap models. Assuming this trend holds for other observed high field radio pulsars, an instrument with the sensitivity of GLAST should see about 40 such sources in high energy gamma-rays from among the known radio pulsars. If the efficiency does not drop to zero for t > 106 years, then the number of detectable sources could be substantially larger. GLAST also has the potential to detect gamma-ray pulsars from nearby galaxies; it would detect about 100 photons above 20 MeV from a Crab-like pulsar in the LMC during a 1 month observation.
The above considerations apply only to young, high-field pulsars. Observationally, very little is known about gamma-ray emission from the much older millisecond pulsars. There is no evidence from EGRET observations (Michelson et al. 1994) of gamma rays from these pulsars, either individually or collectively as might be expected from many such pulsars in a globular cluster. Theoretical models (Chiang & Romani 1992; Chen & Ruderman 1993) of magnetospheric gamma-ray emission from these sources suggest that emission from some globular clusters may be detectable with GLAST. A number of theorists have also suggested the possibility of gamma-ray emission from the interaction of the expected relativistic (TeV) e± wind from the pulsar with the surrounding medium or with the mass outflow from the companion star in the case of a binary (Phinney et al. 1988; Tavani 1991; Arons & Tavani 1993). GLAST observations of globular clusters might detect such emission.
Besides the identified gamma-ray pulsars, there are localized gamma-ray sources observed by SAS-2, COS-B, and EGRET (Kniffen et al. 1975; Hermsen et al. 1977; Fichtel et al. 1993) near the Galactic plane that have no obvious counterparts at other wavelengths. Within 10o of the plane, EGRET has observed more than 30 such sources above 5s. These sources appear to fall into two categories; those with relatively constant gamma-ray flux and a substantial fraction that exhibit significant time variability. Until the recent EGRET detection of periodicity in its gamma-ray emission, Geminga was the most prominent example of the first category; the localized gamma-ray excess in the direction of PSR 1706-44 was another. Of the latter source category, several may be AGNs, but the majority are probably galactic and, therefore, could represent a new source class.
The galactic diffuse radiation is the most prominent feature in the gamma-ray sky. It is highly correlated with galactic structure and much of it likely results from cosmic ray nuclei and electrons interacting with interstellar gas. EGRET observations of the Galactic plane have been compared with detailed models of the Galactic gamma-ray emission to indirectly deduce the Galactic cosmic ray distribution and spectrum. The angular resolution of EGRET limits these comparisons because it is relatively large compared to much of the structure predicted by the models. Preliminary results (Fichtel et al. 1992) for the energy spectrum from the galactic center region already show evidence of changes in spectral slope expected from the nucleon-nucleon component and a steepening of the spectrum at the highest energies. Among the outstanding issues to still be resolved are the relative contributions from various processes as a function of energy and location, the question of cosmic-ray/matter coupling versus cosmic-ray gradients, the physics of high-energy particles in clouds, emission from the Galactic halo, and the contribution from unresolved sources such as the galactic pulsar population (see, e.g., Strong 1994).
Previous to EGRET, only the Orion molecular cloud had been observed and resolved in gamma rays. With EGRET, many nearby molecular clouds, including those in Orion and Ophiuchus, have been detected and spatially resolved (Digel & Hunter 1994). However, with EGRET's sensitivity, the gamma-ray spectrum can only be determined for the entire cloud. In the case of the Ophiuchus cloud, the gamma-ray emission is consistent with the cloud being entirely permeated with cosmic rays with the local density and energy spectrum.
At high galactic latitudes the observed "diffuse" radiation contains both a galactic component and a component that appears isotropic on large scales. This extragalactic component has a relatively steep spectrum (Fichtel et al. 1978). Theories of the origin of this radiation generally fall into two categories: one class assumes the radiation was produced at an early epoch in intergalactic space and is truly isotropic and diffuse while the other class of theories assumes that the radiation is really the integrated flux from a large number of unresolved discrete sources.
The BATSE experiment on CGRO is detecting between one and two gamma-ray bursts per day. The logN-logS distribution and the isotropic angular distribution of the bursts (Meegan et al. 1992) has raised serious questions about models that associate the bursts with a disk population of neutron stars. Models that put the bursts at cosmological distances or in a galactic halo are being seriously considered (Paczynski 1992).
Observations with EGRET have resulted in the detection of gamma-ray bursts at energies much higher than those previously seen. Photons above 1 GeV have now been detected in the spectra of several bursts (Schneid et al. 1992; Sommer et al. 1993; Hurley et al. 1994). Most intriguing is the observation of delayed photons associated with GRB 940217, including one 18 GeV photon 90 minutes after the BATSE trigger (Hurley et al. 1994). There are currently no accepted theories for the source(s) of gamma-ray bursts. The high-energy photons present in the bursts detected by EGRET have further confused the situation as they were not anticipated by any of the existing models.
The EGRET observations of power law burst spectra extending over 3 decades in energy, with no evidence of a high energy cutoff, rule out fireball models that predict modified blackbody spectra with temperature ˜ a few MeV (Goodman 1986; Paczynski 1988), at least for the EGRET bursts. The high energy photons detected and the short duration of the bursts imply g-g pair production above mec2 for isotropic emission models unless the sources are very near. Collimation of the emitted photons due to bulk relativistic source motion is one way to increase the threshold for pair production and allow the sources to be at greater distance (Sommer et al. 1993). The collimation requirements can be severe. For example, 1 GeV emission in the case of GRB 910503 implies gb ³ 13 for galactic halo distances (³ 30 kpc) and gb ³ 565 for cosmological distances (1 Gpc), where gb is the bulk Lorentz factor.
Because the GLAST instrument is essentially a large, programmable high-energy particle detector, it's operating modes can be re-configured and optimized for different scientific objectives. This capability is unprecedented for an orbiting high-energy telescope and presents the possibility of fundamental new discoveries in high-energy astrophysics.
The GLAST design is based on discrete converter planes. Telescope designs have been proposed that use a continuous distributed converter; for example, a drift chamber using high Z gas (Xenon) as the converter. In the multiple scattering dominated limit, we now compare the angular resolution achievable with discrete radiators versus continuous radiators.
In GLAST the radiator and the x-y measuring planes have been placed as close as possible, all within 1mm in depth thickness but a millimeter is still small enough to neglect. The discrete and distributed cases are shown in Figure T1. To simplify the arguments we neglect any errors arising from the finite spatial resolution of the detection planes. In the case of the distributed radiator each sampling layer measures either x or y but not both while in the discrete case each plane gives both x and y. In each case the radiation length is taken to be the same and produce one unit of multiple scattering defined as
qo = 0.014/(pb) sqrt{S} (1 + .038 ln S),
where S is the thickness, in radiation lengths, of a single layer.
Consider the case in which a gamma ray converts in the first layer as sketched on the figure. In the case of the drift chamber the hit recorded in that layer can not be reliably used since angle dependent track corrections can only be made for tracks which cross the entire layer. Hence the first usable measure hit is in layer Y1. The y projection is determined by the next y hit in layer Y2. If we join these two hits by a straight line to estimate the y projected gamma-ray direction we will make an error of
qy = qo {1 + 2/3}1/2.
The first term is due to the multiple scattering between the point of conversion and the first measurement and the second term results from the 2S radiation lengths between Y1 and Y2 (the factor of 3-1/2 relates the projected multiple scattering angle to the displacement angle between the beginning and ends of the track).
Similar logic reveals that
qx = Ã8/3 qo.
The relevant quantity is the area of the error ellipse given by
A =pqx qy = p Ã40/9 qo2.
In computing the same quantities for the discrete case, the x and y projections are essentially identical. Since the gamma ray converts on average half way through the first radiator only Ã1/2 qo of multiple scattering is incurrd before the first x,y measurement. Neglecting the small multiple scattering which occurs in the detectors the next significant scatter occurs in the second radiator, but there is practically no lever arm for this error to act through before the 2nd measurement. Hence
qx = qy = Ã1/2 qo and A = p/2 qo2.
The ratio between the area of the error ellipse for the continuous case and the discrete case is 4.2. Stated another way, for such detectors with radiator thicknesses adjusted to give equal angular resolutions the discrete case will have an event rate approximately 4.2 times larger.
The knowledge of the gamma-ray sky as provided by the EGRET instrument has been used together with an extrapolation for the Log(N)-Log(S) of the gamma-ray sources (again accounting for the currently observed EGRET sources) as input to a simulation program to illustrate the capabilities of GLAST relative to those of EGRET.
The simulation program has been developed as part of an effort to extract the Log(N)-Log(S) distribution of the extragalactic gamma-ray sources through fluctuation analysis of the EGRET high-latitude diffuse background data. As input, this program is fed a given scenario of diffuse emission and added point sources. Using the known instrument response functions (effective area, point spread function, etc.) it then simulates what the observed gamma-ray counts and intensity distribution will be for a given exposure. These simulations provide test environments in which analysis programs can be checked for their capabilities of reconstructing the parameters of the 'true' input sky by applying them to the simulated 'observed' data.
Here the simulation is used to demonstrate how the 'observed' data look for a one year all-sky survey, with exposure distributed uniformly over the full sky, when measured with GLAST and, for comparison, when measured with EGRET.
To construct the tentative 'true' sky, a diffuse emission model that is derived on the basis of EGRET data and gas tracers (Bertsch, et al. 1993), and the EGRET catalog of sources (Fichtel, et al. 1994) is used. The population of weaker extragalactic sources that are below the EGRET detection threshold is created in agreement with a theoretical extrapolation of the observed Log(N)-Log(S) distribution (Salamon & Stecker 1994), which is based on the EGRET catalog and on assumptions about the nature of the EGRET source population (Fichtel, et al. 1994). These sources are statistically distributed over the sky.
The procedures for creating the 'observed' EGRET and GLAST skies are the same with the following exceptions: in the case of EGRET, the instrument parameters for sensitivity and pointspread distribution are derived from calibration data; further the actual exposure for the 'EGRET Phase 1' all-sky survey is used. In the case of GLAST, the instrument parameters are derived from the instrument simulations described in section 3 and the exposure is assumed to be uniform across the sky. The total observing time for both cases is about equal.
Figure B1 shows the Log(N)-Log(S) distribution from which the sources are synthesized. The irregular solid curve shows the Log(N)-Log(S) measured by EGRET. The dashed extrapolation describes the Euclidean case which, as indicated by the horizontal upper limit, would be in conflict with the observed diffuse emission level unless it is cutoff as indicated. The solid and dotted curves indicate the range possible according to the model of (Salamon & Stecker 1994). The prediction indicated by the full line has been used for the simulation. The dashed vertical line indicates the minimum source intensity for which sources were created in the simulated sky.
The simulation is done with the following procedure:
Figure B1. Log(N)-Log(S) distributions. Irregular solid curve is the Log(N)-Log(S) measured by EGRET for sources above a 4s detection threshold. The dashed curve is the Euclidian extrapolation of the EGRET distribution. It is cutoff so as not to conflict with the observed isotropic "diffuse" level. The solid and dotted curves indicate the range possible in the model of Salamon & Stecker (1994).
Figures B2 (a) and (b) show the simulated data for both instruments after convolution with the pointspread functions but without the fluctuations introduced by photon counting statistics. Figures B2 © and (d) show the 'raw data' intensities actually observed when photon counting statistics due to the finite exposure are included. The scale for for (a) and © is the same as is the scale for (b) and (d). It is evident that the number of sources clearly visible by GLAST is orders of magnitude larger than for EGRET. For purposes of illustration, only galactic latitudes > 0o have been populated according to the Log(N)-Log(S) distribution of Fig. B1. For latitudes < 0o, the "isotropic" diffuse radiation has been modelled as truly diffuse and the only point sources included are those in the first EGRET catalog.
In Figure B3 sections of the same maps are displayed in a different manner which gives a clearer impression of the capabilities that GLAST will have for observing regions of strong emission where EGRET is limited by source confusion problems. Note how clearly the gamma-ray source at the galactic center and also the pulsar PSR 1706-44 are observed and resolved. Many more sources will be resolved along the galactic bulge which so far are invisible to EGRET due to source confusion and insufficient number of counts.
Figures B4 compares GLAST's capabilities with those of EGRET for the Virgo region where a 'deep' survey has been performed by EGRET. To account for GLAST's much finer angular resolution, particularly at high energy, the pixel size for the GLAST images is taken to be 0.05 degrees which is 1/10 of the 0.5 degree pixel size of the EGRET image. The dramatic gain due to better angular resolution and sensitivity is evident. The extension of the observable Log(N)-Log(S) range by GLAST will substantially narrow the number of acceptable theoretical models.
It is to be noted that image analysis procedures such as crosscorrelation analysis, likelihood analysis, or maximum entropy reconstruction are usually applied to data such as shown in © and (d) of Figures B2 and B3. These methods are able to extract much more information than is immediately apparent to the naked eye. However the 'raw pictures' shown here indicate how the quality of observations with these instruments compare.